仏教思想の根幹を数学で解釈する
今まで何度となく考察してきたのですが、「この世で作られた一切は変化する」とか「この世の一切の現象は縁起で生起する」という仏教思想の基本の考えは、当時としては、きわめて卓越した考えなのです。
ただし、基本の考えといっても、時代とともにその道理が実証され、時代に即してより精緻なものに変化するのが普通なのでしょう。すなわち「どのように変化するのか」とか、「どのように縁起が作用して、一切の現象が生起するのか」という「仕組み」や「構造」が、ほとんど究明されてないのです。
この「変化」とか「縁起」、さらには「空」とか「悟り」の究明に、最も役立つと思われるのが前回、前々回で考察しているように、一時期に古代インドで発展し、そして西欧で確立された数学なのです。
「変化」を表現する言語、数学
「諸行無常」は、「この世で作られた一切は変化する」という意味です。変化するとは、時間の経過にともない位置や量が変わることですが、これらはすべて数字で表現できるのです。
紀元前500年頃の人で、ギリシアの哲学者・数学者であるピタゴラスは、「万物は数である」と言ったそうです。
このような古代人の卓越した発想も、実は13世紀末~15世紀末のルネサンスまでの約2000年の間は、大きな進展はなかったのです。この間は、神も自然界も精神界もすべて一つの体系として思考がなされ、また「変化しない」ものが重視されていた時代であり、数の計算やその幾何学的な図形も、一般言語と同様に、静的・固定的な表現として取り扱われていたのです。
これを一変させたのが、近代科学の父といわれるガリレイ(1564~1642)や近世哲学の祖、解析幾何学の創始者、デカルト(1596~1650)なのです。
デカルトの代数学についての最大の功績は、自由自在に変化する文字記号「変数」という概念を生みだしたことです。これ以前にも数の代わりに記号を用いている場合もあったのですが、これはある特定の数を表現するためのものであって、時間が経過しても変わることはないのです。
すなわち、変数Xは、直線上のある一点でなく、直線上を自在に動かすことができるようになったということです。これは何を意味するかというと、今では誰も知っていることですが、この変数Xが原因となって、何らかの変化が生まれるとしたら、これを変数Yとします。いまXが移動する直線(X軸)とYが移動する直線(Y軸)とを直角に配置したら、原因としての変数Xの変化によって、その結果としての変数Yの変化を、目で見える図形として表現できるということです。
後に、変数Yは、変数Xの関数(「縁起」)であるという、記号のみで表現される関係式として、関数の概念が生まれるのも当然の帰結だったのです。
上記のようのように、数式だけで表現される関数の変化のパターンを目で見えるようにするには、図形が有効であり、逆に幾何学図形を研究するのに、数式による関数のみで思考ができることです。
このように、デカルトが解析幾何学の創始者と言われるのは、形状と数式との相互変換による思考を可能にする「変数」という概念を生みだしたからです。これは一見、静的・固定的と考えられる形象を、数を用いた変化で表現できることを実証したとも言えるのです。
いみじくも、原始仏教で、「諸行無常」とか「縁起」という発想が、2000年後に、「変化」を表現する数学という言語で、具体的に思考が可能になり、これ以後、この世の一切の具象や現象に対して、如何に広範囲に適用できる関数(縁起)が解明できるか、またその結果として新たな具象や方法が創造できるか、という研究が数学やその応用分野で続けられてきたのです。
ここで、この世の具象や現象を、「変化」を表現する数学で思考する意味について、少し説明しておきます。
この世の具象や現象は、まさに無数にあり、これらが「縁起」で生起することを実証しようとしても、事実上不可能なのです。この世の具象や現象は、当時としても、かなり細分化されているものであり、この数を大量に減少させるには、細分化される以前の状態に戻す必要があるのです。すなわち統合化とか普遍化をする必要があるのです。
仏教では、この統合化をどのように処理したかというと、井筒俊彦「意識と本質」((株)岩波書店、1991)の記述(p146)を引用して説明します。
『第一段は禅の道に入る以前の時期。当然、彼は普通の人の普通の目で、自己の外なる世界を眺めている。山は山であり、川は川。世界は有「本質」的にきっぱり分節されている。・・・山は山の「本質」によって規定され、川は川の「本質」によって規定されているからだ。
ところが、参禅して、一応見性し、ある程度の悟りの目を開いて見ると、世界が一挙に変貌する。・・・それまで、いわゆる客観的世界をぎっしり隙間なく埋めつくした事物、すなわち「本質」結晶体が融けて流れだす。存在世界の表面に縦横無尽に引きめぐらされていた分節線が拭き消される。・・・山はもう山ではないし、川はもう川ではないのだ。そして、そんな山や川を客体として自分の外に見る主体、我、もそこにはいない。すべてが無「本質」、したがって無分節、もっと簡単に言えば「無」なのである。・・・
第三段階は再び「有」の世界。第二段階で一たん無化された事物がまた有化されて現れてくる。・・・』
このように、仏教で統合化することとは、禅定して悟りの境地に近づくことなのです。そして究極の「無」の状態まで達してしまうのです。この過程で「縁起」も無化されてしまう訳で、「縁起」の構造が何なのかなど、究明する必要はないのでしょう。ただし、今までも考察していますが、「無」から創造的な「有」を生み出すには、深層意識を拠とすることになるので「意味不明」の現象を扱うことになり、天才的な洞察力の持ち主でない限り、至難の業なのです。
この点、凡人でも勉強さえすれば実現が可能な数学の方法を説明します。
この世の具象や現象のままでは、凡人にはわかりやすいのですが、小学校で習う算数のようなもので、高度の応用は期待できないのです。ただしこれとても思考のための訓練として、さけて通れないのです。
これは、この世の具象や現象を、数として表現するための訓練なのです。この世の具象や現象が「変化」するものであるならば、「変化」とは、時間の経過にともない位置や量が変わることですから、すべて数で表現できるのです。
これは、この世の具象や現象から、変化を表現する基となる数のみを抽出して、抽象化して表現するということを意味します。数学で思考するとは、この世に無数にある具象や現象を、抽象化し、数のみでその関係性を究明する学問なのです。
このように、数学で思考するということは、この世の具象や現象を、抽象の関係性の世界に変換し思考する作業と、その結果得られた抽象的な関係をこの世に当てはめて(具現化して)、新たな具象や方法を創造する作業をいうのです。これを下図(図1)に示します。
なお、現実の世界の具象が、抽象の関係性の世界に変換される様相を、形而上学者ともいわれる井筒俊彦は、それぞれ「本質」で固められた結晶体が融けて流れだし、その分節(輪郭)線が拭き消される、ときわめて印象的な表現をしているのです。
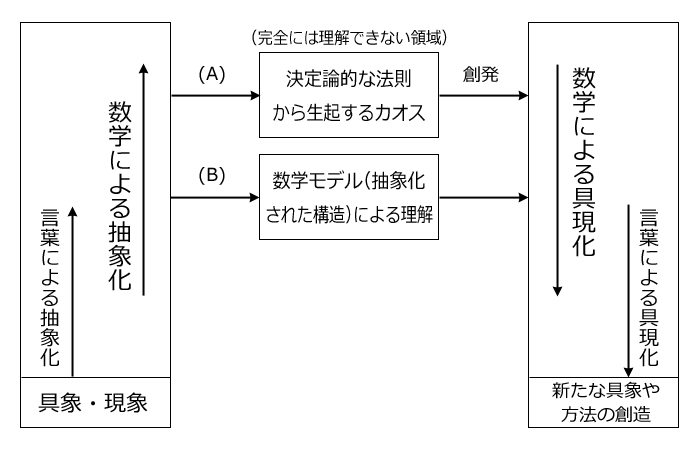
図1.数学における思考の経路
図1で、数学の関係式は、最初の段階では、適用範囲が狭くかつ複雑な構造として表現されるのでしょう。しかし抽象化の思考を重ねるうちに、より広範囲に適用でき、かつより単純化した、構造的にも美しい関係式に改良がなされるのです。これは抽象化の度合いを高めるという作業です。
数学の専門家による高度に抽象化された関係式などは、私のような凡人には、ほとんど理解できず、これを具体的に言葉で説明することは困難なのです。
私など一般の人が、関係式の意味が理解でき、自由自在に応用ができるためには、抽象化の度合いをある程度低くした(具現化した)、すなわち適用範囲を限定した関係式を利用することになるのです。
図1で、(A)の経路、すなわち簡単な関係式からカオスか生起する場合については、これまでこのHPで何度となく考察してきましたので、簡単に説明します。最初にカオス現象に気づいたのは、1890年代であり、天才的な数学者アンリ・ポアンカレの洞察力によるものですが、これから約70年後の間、すなわち電脳がやっと使える状態になるまでは、この論文を誰も評価できなかったのです。
カオスの研究が盛んになったのは、電脳が急速に発展した1970年代であり、我々一般の人がパソコンで、マンデルブロー集合の不思議な画像が作成できるようになったのが、1980年代以降です。
要は、カオス現象の研究には、電脳の助けを借りないと不可能なのです。
鈴木大拙の「仏教哲学における理性と直観」
鈴木大拙全集((株)岩波書店、2000)の中で、私の好みでよく引用するのが、第十二巻の「禅の研究」の四、「仏教哲学における理性と直観」です。
ここで記述されている内容を、図1の数学による思考の経路に対応させて表示すると、下図(図2)のように表せます。
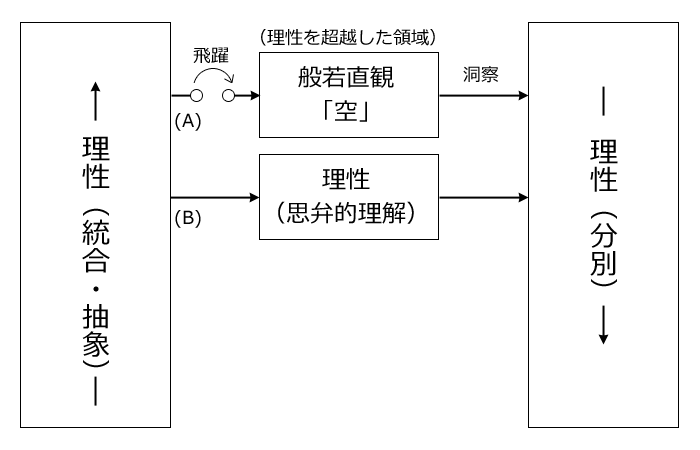
図2.鈴木大拙「仏教哲学における理性と直観」(1951)
この内容は1951年に記述されたものですが、この内容で特に注目に値するのは、「縁起」すなわち因果関係は、「般若直観」すなわち「空」ではなくて、「理性」として記述されていることです。
次に、図1と形式的にはよく対応がとれていることです。これらは、鈴木大拙の合理的精神の現れなのでしょう。
次に、考察を必要とする箇所の記述(P108)の一部を下記に引用します。「般若直観」の本質を、月と水に譬える譬喩で説明した後、『けれどもこの譬喩は誤解されぬとも限らぬ。無限に分けることができるにも拘わらず、月の本体というものが一であるという事実から、般若直観もやはり多から抽象された一を暗示しているものと思われやすい。けれども、こういう具合に般若の性格を規定することは、取りも直さず、般若を破壊することになってしまう。般若の単一性・完全性あるいは自己充足的性格などは、もし我々の分別意識に投影することを止むをえないとするならば、上記の性格は、決して理論的にまたは数学的に解釈してはならないのだ。』
まず最初の下線について、「般若直観も・・・と思われやすい」と記していることから、「多から抽象された一」と言う記述は、「理性」の領域を意味するものです。この下線の意味は、「般若直観」の場合は、「理性」と同じと思ってはならないということです。
二番目の下線について、1951年では、図1の「決定論的な法則から生起するカオス」については、全く知られていなかった時代ですから、この領域を数学で解釈できないとするのは当然のことなのです。そして現在でもこの経路(A)は、理論的には制御できない領域なのです。だから下線の記述は図1と矛盾している訳ではないのです。
要は、「般若直観」の性格は、直観で対応されるべきもので、「理性」のように『まどろしい、入念な煩瑣(はんさ)な弁証の過程を経た上のことではない』と言っているのです。
以上のように、鈴木大拙のこの論文は、現在でも十分に納得のいく記述であり、高く評価されるべきものです。
「機械的」という言葉に潜んでいる意味
今回のテーマは、別な言い方をするなら、仏教思想を数学者としてのデカルトの思想で解釈するということでした。さらに別な言い方をするなら、文系の人が最も軽んずる言葉の一つとして、「機械的」という言葉についての考察だったのです。
「機械的」という言葉を広辞苑で引くと、
① 機械が動くように単調な動きを見せるさま。
② 個性的ではなく、型どおりのさま。
③ 力学的。力学の法則に還元できる過程についていう。
特に①と②は一見人間として好ましくない表現のようですが、ここには人間として必要な深い意味が潜んでいるのです。
①は、「機械的な単調さ」と言う言葉が気になるのですが、実は、これが人間が最も理解できる構造なのです。どんなに複雑で難解な事物でも、例えば目に見えない化学反応や電子の流れにしても、略図とかブロック線図のように、核心以外を一切取り省いた(抽象化した)関係図式、即ち機械的な構造で表現することで、人間は容易に理解できるのです。
頭脳による仕事と言っても、元を正せば、機械的なのです(機械的構造(決定論的構造)からカオスが生起することを前提として)。人間が自然から作られた以上、その基本構造は機械的なのです。
②の「個性的」とは、細分化(特殊化)されたことを意味し、「型どおり」とは、統合化(普遍化)されたことを意味します。すなわち事物を、細分化した状態で考えるか、統合化されたモデル(手本としての雛型)をたたき台として考えるか、ということです。
何事によらず、勉強するとは、この「基本の型」を理解することなのです。これを知らずして、個性的などと言う資格はないのです。
③については、このHPでの何回かの考察の通り、仏教思想とよく似ていて、日本が世界に誇れる「いろは歌」の意味でもあるのです。「諸行無常」とこの拠となる「一切の現象は縁起から生起する」とは、③に対応できるのです。
仏教では、静的・固定的なものより、動的変化に視点を置き、縁起とは、この変化を起させる仕組みとか機能を意味するのです。「還元」とは、根元に復帰させること、すなわち一切の事象をその根元に立ち帰って動きとして捉え、その機能を思考し、一切を理解することで、迷いを滅することなのです。
そしてこの③はデカルトの数学的な思想でもあるのです。これを「還元主義的機械論」と呼ぶそうです。この思想を背景に、この後、アイザック・ニュートン(1642~1727)によってニュートン力学の法則として確立されるのです。これは地球の引力下にある一切の物体の正確な運動法則を数学的に公式化し、さらに天体にまで拡張できることが明らかになった自然科学として画期的な思想だったのです。
以上のように、「機械的」という言葉は、人間がこの世の事象を理解する上で、重要な意味を持つというのが、私の主張です。