対立構造の共存する世界（文章）

前回に引き続き、「即」の概念についての感想を述べさせていただきます。

「即」の意味

「即」を広辞苑（第五版）で引きますと、語訳の分類の一番目に「①つくこと」とあり、三番目に仏教用語として「③[仏]相反する2物がそのまま同等で差別のないこと。相即。」と記されています。③の「相反する2物」というのは、例えば「自己と他者との対立」を考えることができます。即ち自己も他者も同じ人間ですが、その考えや意見が異なる場合です。

古今東西、対立や紛争は絶えることがありません。仏教思想ではこれを防ぐための智慧として、対立する意見を一本化する（一体化して差別をなくす）、「即」の概念があります。ここではこの対立する意見を一つにするための方法を詳細に検討してみます。

どちらかの意見に従う。
これは「無我」などの思想に基づくもので、どちらかが譲歩して、相手の意見に従うことです。
両者が歩み寄り、その折中案をとる。
これは他者を思いやる「慈悲」の思想に基づくもので、相互に思いやりその中間案をとることです。
両者の意見を併記して、曲がりなりにも一本化する。
これは「六相円融義」に見られるような、個々の意見を尊重し争わずして共存し、協調して新たな秩序を構築していこうという思想で、もちろんその根底には「無我」や「慈悲」の思想があります。

以上のことを幾何学的に表現してみましょう。これには力の釣り合いなどで用いられるベクトル、即ち大きさと方向をもつ矢印の付いた線分で表現できそうです。意見が異なるとは、ベクトルが異なることと見なし、これを一本化することは、これらのベクトルの和をとることに相当します。

例えば、自己と他者の対立構造を二つのベクトルで下図（Ⅰ）ように表します。ここでベクトルの長さは両者同じで向きが60°異なっています。即ち考え方に60°のひらきがあることです。

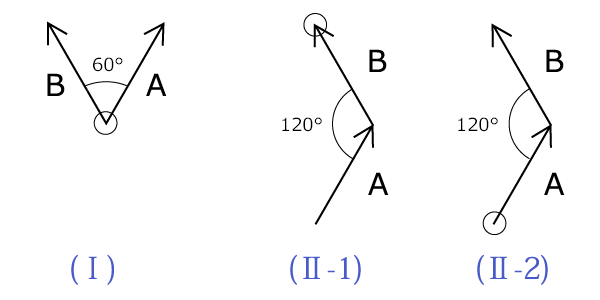
上記の１はいずれかの意見を無自性（空）としますから、残りの意見のベクトルが有になります。

２は二つのベクトルの和（A+B）としての新たなベクトルが有となり,これのみが表されます。ベクトルとベクトルを加算するとき「和」という言葉を用いますが、これはたいへんに含みのある言葉なのです。３の場合は、この和とせず、それぞれのベクトルをそのままくっつけて、曲がりなりにも折れ線の状態で一本化することです。即ち図（Ⅱ-1）,（Ⅱ-2）のようにベクトルを置き換えても問題ありません。

複雑多様なこの世の中、一本の直線ですっきり表現できる現象など、きわめてまれな存在で、いろいろなあつれきによって幾重にも折り曲げられても、存続するためにはやむおえないというのが、本来の姿なのでしょう。３はこれを良しとする思想なのです。ただしこれはあくまでも外見上のことで、両者の顔を立てて、二つのベクトルを記録に残しただけで、実質上はその和として一本化されうるものでしょう。

コッホ曲線とその作り方

下図（n=4）を見て下さい。無数の折れ線が一つにつながっています。多と一との関係を表す相即･相入の概念と相通ずるようにも思われます。実はこの図形はコッホ曲線と呼ばれ、画面上ではこれ以上細かにするとぼけてしまいますが、厳密には無限に小さい折れ線が無数個存在する状態をいうのです。そしてフラクタルに関する書籍で、フラクタルとは何かを説明するための典型的な例なのです。

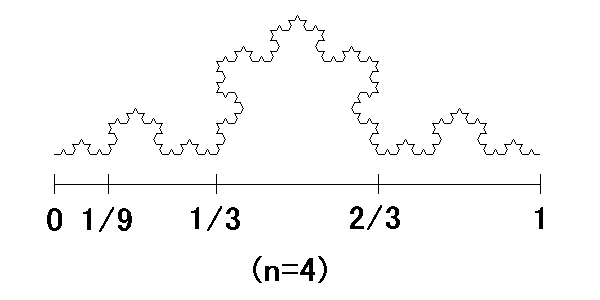
この曲線の全体の形の中にそれと相似な図形がいくつも含まれています。最もわかりやすい位置で説明しますと、0から1/3までの区間の図形と全体の図形とは相似ですし、0から1/9までの区間の図形も全体と相似です。これはどこでも、もっと小さな区間の図形でも拡大すると全体の図形と相似になるのです。これを自己相似性をもつ図形といいます。

このようなコッホ曲線の作り方にはいろいろありますが、次にその一例を示します。

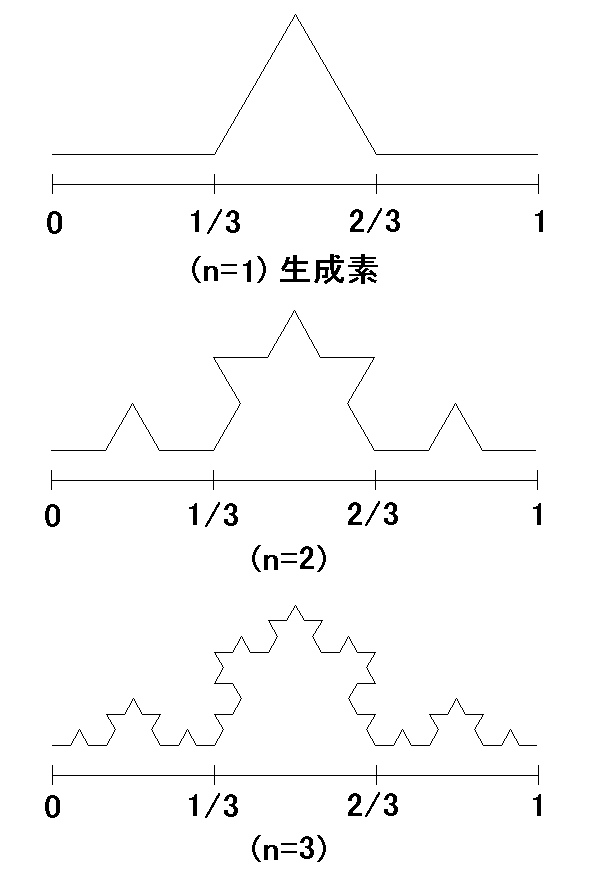
まず下図（n=1）のように、0から1までの区間を3等分し、中央の1/3の部分に同じ1/3 の長さの正三角形の上部の二辺を置いた、四本のベクトルから構成される図形が、コッホ曲線を作る基本となる図形で、これを生成素と呼びます。

以後この生成素の分身を作ることを考えます。分身とは自身が二つ以上の縮尺された自身に分かれることです。図（n=1）は４本のベクトルから構成されていますから、いま1本のベクトル上に1つの分身を作るとすると、４つの分身が作れます。ここで各ベクトルの長さは 1/3 ですから、生成素を 1/3 に縮尺して、各ベクトルと置き換えます。これが図（n=2）です。この図形のベクトルの本数は 4x4 の 16本で、各ベクトルの長さは1/9で、そこで生成素を 1/9 に縮尺して、16本の各ベクトルと置き換えたのが、図（n=3）です。これを無限に繰り返したのが、コッホ曲線となるのですが、実際にはプリンターの解像度からn=4 以上は明確に判別できなくなります。

コッホ曲線の新たな解釈

フラクタルの典型であるコッホ曲線と相即･相入の概念との関係について考察を加えます。

まずコッホ曲線の生成素の意味づけです。自己と他者の対立する意見を一つにする方法の３、即ち両者のベクトルをそのままくっつけて、曲がりなりにも折れ線の状態で一本化した、（Ⅱ-1）を○印を中心に時計方向に60°回転したものと、同様（Ⅱ-2）を時計方向に120°回転したものを○印の位置でくっつけ一つにしたのが下図で、これはコッホ曲線の生成素に相当します。

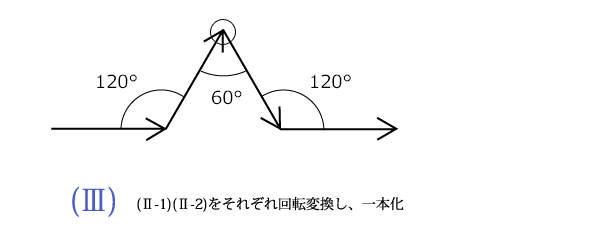
このコッホ曲線の生成素は、対立構造（Ⅰ）のそれぞれのベクトルを残したまま一本化（即）した二組のベクトル表現（Ⅱ-1）,（Ⅱ-2）を、さらに巧妙に変換し、つなぎ合わせて一本化（即）したもので、形としては単純で左右対称の「角が立つ」構造です。この構造も対立構造を思わせ、この「角が立つ」構造が無数に連続（共存）する世界がコッホ曲線なのです。

コッホ曲線は、1904年スウェーデンの数学者ヘルゲ・フォン・コッホによって、あらゆる点で接線の引けない曲線即ち微分不可能な曲線として提示されたと言われていますが、当時はきわめて特別なものとして、あまり評価されなかったようです。しかるに近年ではこれがリアス式海岸やごつごつした山岳など自然の本質としてどこにでもあることが明らかとなり、かつ自己相似集合のわかりやすい例として、脚光を浴びたのです。

この自己相似集合は、何本かのベクトルで構成される生成素を縮尺して一本のベクトルと置き換えることを何度も繰り返すことで作りました。ここで「置き換える」とは、置き換えるベクトルを消去して（無自性にして）、そこに縮尺した生成素を入れることに対応し、これは「相即･相入」を意味します。即ち画像目次「相即･相入/事事無礙」でも記したように、生成素を縮尺して「相即･相入」を幾重にも繰り返すことで構築される構造が自己相似集合（フラクタル）なのです。そしてこのフラクタル構造に、「華厳経の風景」からも明らかなように何らかの「美」の秩序が存在することを経験してきました。

思想や宗教の異なる多くの人間が争わずして共存していく秩序ある世界に思いをはせるとき、このコッホ曲線や相即･相入の概念は意義があるように思えるのです。