円相、花から果実への移行

前回は「角が立つ世界」についてフラクタルから考察しましたが、今回は「角がゆるやかな世界」を考察します。

禅宗でよく用いられるという「円相図」があります。これには「角」が無く、始めも終わりもなく、きわめて円満な世界です。円相図は心、仏性や悟りの境地、宇宙などを表現すると言われています。

円を線分で表現するには多角形を用い、角の数を多くすればするほど角がとれ、無限個の角の数のときが円なのです。即ち円は完成された状態であって、凡人には近寄りがたいところがあります。そこでまだゆるやかな角が残っている多角形で近似した円のほうが、凡人には扱いやすいのです。

また前回のような自己相似集合の作り方の手法を用いるには、線分の集まりとして表現する必要があるのです。

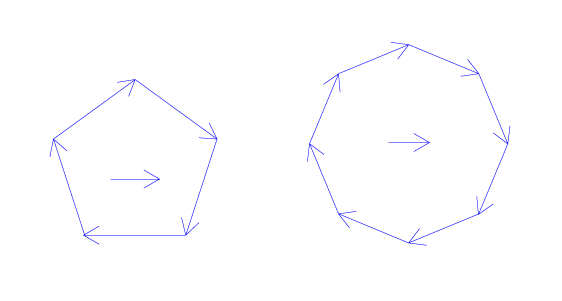
今回展示した画像は、円相を描くような方向にベクトル表示した正五角形と正八角形を生成素にしたときの自己相似集合で、正五角形がn=6、正八角形がn=5の場合です。この生成素は下の図1に示していますが、いずれの生成素ともその中心近傍に一本のやや短い線分のベクトルが追加されています。

ところで仏教関連の書籍を見ていたら、臨済宗の僧、沢庵（1573-1645年）の円相図に遭遇しました。この円相図、宇宙を表現していると説明されていますが、円の中央の近辺に小さな「レ」の字が墨で描かれていました。これには何らかの由来があるのかもしれませんが、不勉強の私には解りません。

フラクタルの世界で花を探して求めている私には、この「丸書いてちょん」の「ちょん」にはきわめて重要な意味があるのです。花の造形の観点からは花の正面となる円形に対して、めしべとおしべの付け根となる花心がないと、間が抜けてしまうのです。即ち花のような構造を作るための自己相似集合の生成素としては、多角形の中央付近に小さな線分を一つ入れると、より花らしくなるのです。

なぜこのような生成素で、展示画像が生み出されるかの説明を正五角形の場合について示したのが下の図2の（n=2）と（n=3）の過程です。前回説明した通りり、（n=2）は生成素を縮尺して、生成素を構成する各ベクトルと置き換えたものです。

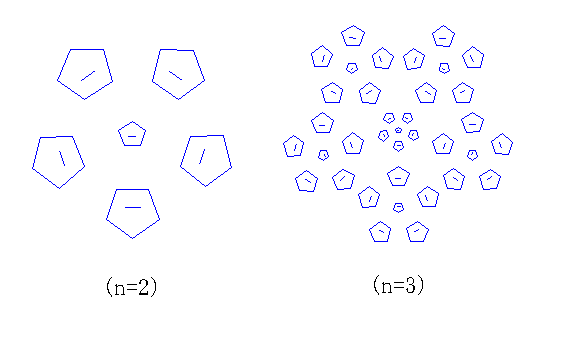
以上、円をおおざっぱに近似した多角形を生成素にすると、その自己相似集合は展示した画像のような花模様になるのです。これも華厳の宇宙を表しているのでしょうか。

ここで、もうみなさまも気が付かれたと思いますが、生成素として多角形の角の数をさらに多くし、角を滑らかにするほど（円に近づけるほど）その自己相似集合の形状は、花模様ではなくなり数珠のような円になり、そして最後はただの円になるのです。

これについては、花から果実に移行する過程を意味していると私は解釈しています。「角」が無くなれば即ち「円」となれば、修行は完成したものと解釈できます。花は修行の功徳を意味し、仏の修行時代を物語るものなのでしょう。

「華厳経探玄記」では「仏華厳」という言葉について、「仏とは及ち果円（まど）かにして覚満するをいい、華とは万行を開敷するに譬え、厳とは茲（こ）の本体を飾るに喩う。」文献（１）と書かれています。

今回の次のステップとしては、 「角」の無い「円」の世界、即ち円教や円融無礙の世界をフラクタルで考察することになります。基本的には、円の中に円を相即・相入するフラクタル,「相即・相入/事事無礙」で考察していますが,仏の悟りの世界を究明するにはまだまだ不十分・不勉強で、今後時間がかかりそうですが,さらに考察を進めます。