自己相似集合の世界観

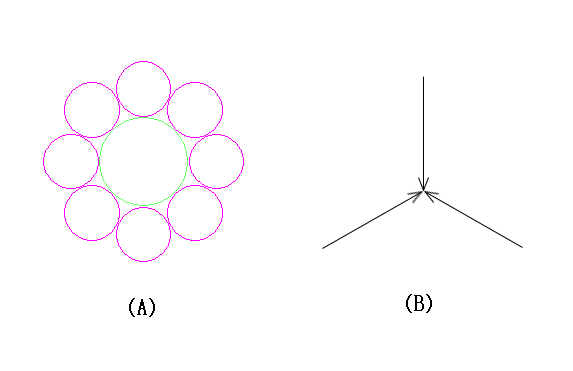
今回の展示画像は、一つの円を中心にその周囲に八つの円から構成される合計九個の円を生成素(図1(A))として、これを一つの円の中に相即・相入し、これを3回繰り返した自己相似集合の図形です。さらに繰り返して、もっと小さな円を入れ込むことも可能ですが、繁雑になるのでこの程度にとどめますが、完全な形は無限に繰り返した場合です。これは前回の展示画像と同様に幾何学的に完全な自己相似集合の図形です。
前回と今回の画像を目をこらしてじっと見ていると、ある限られた領域に、その領域の形状よりも小さな無数の相似の集合で構成され、かつきわめて秩序正しく均等に配置されていることが判ります。
そして普賢菩薩の毘廬舎那仏の世界について語る偈文(げもん)「一つの毛孔のなかに、無量のほとけの国土が、装いきよらかに、広々として安住する」とか「一つの微塵のなかに、あらゆる微塵のかずに等しい微細の国土が、ことごとく住している」文献(1)の文章のイメージが、あざやかに浮かび上がるのです。
華厳経を勉強して最も不思議に思うのは1500年も前の昔に上記のような文章がなぜ書けたのであろうということです。普通凡人には何らかのイメージがないと、このような文章は書けませんので、華厳経の作者は天才的な頭脳を持っていたとしか私には考えられないのです。
さて本論に入ります。「相」の意味は広辞苑(第五版)によると、①外見、形状 ③あいともに、互いに ⑤[仏]性質、特徴、現象的なすがた などあり、単に形だけでなく外に表れる性質なども含まれると考えられます。
「自己相似」の意味を自己と他者とが相即・相入し合い、相互に依存する関係にある人々と考えることもできます。ところで幾何学的な自己相似集合の図形は、生成素をその生成素の構成要素の中に相即・相入することの繰り返しで形成されるのでした。この生成素を自己及び他者あるいはこれらの世界と考えると、自己と他者あるいは自己と世界(全体)の差別はなく、他者や全体の中に相即・相入した自己を見出す世界観が浮かび上がり、自己も他者もその全体も調和の視点で相似の集合体と見なせます。
以上自己相似集合の世界は、自己を全体の必要不可欠の構成要素として位置付け、かつ他者と全く平等であることを明示する構造なのです。
文献(1)の「重重無尽の縁起の教え」の項で、「十玄門」について「・・・、 自己についても、本来、他者の要素を自己の中に豊かに有しているのであり、 世界の中の一存在であると同時に、もとよりあらゆる他者に開かれた存在であることが見えてくることでしょう。・・・ この自己がかけがえのない自己であるがゆえに全体なのであり、かつ他のあらゆる主体と相即・相入していることを思うべきでしょう。」と記述されています。
なお自己相似集合図形が華厳の思想になじみやすい事例をもう一つ挙げると、展示画像の背景は、因陀羅網を意味する網の目構造の自己相似集合です。この華厳思想を具体的に表現している網の目構造は、三本のベクトルが一点に集束するような生成素(図1(B))の自己相似集合として容易につくれます。この生成素の三本の線分(ベクトル)は、あたかも三本足の鼎(かなえ)のように、いずれが主でもなく従でもなく、互いに補い合って依存しています。
「フラクタル(Fractal)」という用語は、1975年にベノワ・マンデルブローが新たに考案した言葉であり、語源は不規則を意味するラテン語のfractusで、小片、断片、微小、破片などの意味が含まれるといわれています。これらの意味にはさらに深い意味があるものと考えられますが、これについてはまた別の機会に説明します。ここではより一般的な意味について記述します。フラクタルについて、文献(3)の招待論文の中でマンデルブローは下記のように記しています。
「自分でフラクタルと呼んだ形状はすべて「ざらざらしていて自己相似的」という性質をもっていた。 相似といっても必ずしも幾何学的相似の意味はなく、「似ている」といったつごうのよいゆるい意味である」。
フラクタルという言葉 を学術用語として難しくとらえるよりは、自然界や社会のモデルとして、もっと身近な存在としてとらえたほうが役に立ちそうです。マンデルブロー自身これを多くの欲望が対立する株価の変動モデルとして応用しています。
ここでは,この「ざらざらしていて自己相似的」という世界は、前々回及び前回でも検討したように、多かれ少なかれ自我をもつ善男善女の住むこの世を表していると考えてもよさそうです。この世界は自然界の現象も含めて現実社会の複雑性があり、きわめて魅力的なのです。
これに対して今回展示したような滑らかな円の幾何学的自己相似集合の図形は、比較的単純な構造のため基本的な世界観を説明するときには役立つのですが、完成度が高すぎて(秩序が良すぎて)、 創造性という面からはあまり面白くないのです。
このように自己相似集合図形と言っても、簡単な手法で作ることができる幾何学的な図形と、 漸化式による決定論的カオスから生まれる「華厳経の風景」で見られるような、局部的な自己相似性をもつより複雑で創造性の豊かな図形とがあります。