鈴木大拙「華厳の研究」の研究

漸化式(ぜんかしき)の意味
みなさん、f(f(x))の意味がおわかりですか。
高校の数学で、2つの変数xとyの間に何らかの関係があって、xの値が定まれば、これに応じてyの値が定まるとき、yを「xの関数」といい、y=f(x)と表わします。ここでf( )は、いわば何らかのfunction(機能、作用)が与えられる容器のようなもので、このカッコの中にxを入れ込むと、yになれるのです。
これはまさに「相即相入」の概念によく似ていいると思われないでしょうか。 ここで、f( )にf(x)を入れたf(f(x))は、「「xの関数」の関数」ということになります。 さらにこれを無限に「反復・繰り返し」を行うと、・・・f(f(f(f(x))))・・・、すなわちxの関数の関数の関数の・・・ということになります。 ただこの様に表現すると、わかりにくくなるので、変数Xに下付きの添字を付けて、X0, X1, X2, X3, ・・・Xn, Xn+1とします。ここで最初のXをX0とし、次のX1をf(X0)と表わしています。
すなわちX1=f(X0)、X2=f(X1)=f(f(X0))となります。したがって、
X3=f(X2)=f(f(X1))=f(f(f(X0)))です。これを一般的に表現したのが、
Xn+1=f(Xn)
この式は今までに何度も登場してきた漸化式の基本形です。
Xn+1=f(Xn)
=f(f(Xn-1))=f(f(f(Xn-2)))=・・・
=・・・f(f(f(X0)))・・・
すなわちXn+1は、Xn, Xn-1, Xn-2,・・・X0がそれぞれ「相即相入」していることになり、それぞれ一体化して、今ここにおいてXn+1として成り立っていることを意味します。そしてこの漸化式は、まさに「関数f( )の入れ子構造」であり、「相即相入」を何度も「反復・繰り返し」たときの結果を示すものなのです。
すでに「相即相入/事事無礙(じじむげ)」で検討しましたように、基本的な自己相似集合図形の作り方は、この「相即相入」を何度も「反復・繰り返し」することでした。今回の展示画像も全く同様の方法で作られたものです。
今回の題目でもあります「鈴木大拙「華厳の研究」の研究」は、厳密には正確ではありません。正確には「華厳の研究」の研究の研究の・・・なのです。
すなわち最初に鈴木大拙「華厳の研究」を研究した大先輩がこの影響を受けて、新たな論説を生み出し、それを中先輩が受け、再度考察し、さらに小先輩が再度考察した結果が私の知識となり、これを基礎として「華厳の研究」を再度考察する訳です。この「反復・繰り返し」によって、すなわち多くの人が一体化することで、物事が徐々に変化していくのです。これを「漸化」というのでしょう。また生物の「進化」と考えてもよいと思います。
鈴木大拙「華厳の研究」
鈴木大拙全集、第五巻((株)岩波書店、2000年5月)の「華厳の研究」の第二篇の「華厳経に於ける場面の全面的転廻」で次のように記述しています。
『「華厳経」に来ると大乗仏教という大宗教劇の演じられる舞台面に完全な変化がある。・・・目にうつるあらゆるものが、すべて皆、たぐいのない光に輝きいでるからだ。われわれはもはや、暗い、硬い、そして限りのあるこの地上の世界に居るのではない、 不可思議にも身は運ばれて天上の銀河の間に上る。この天上の世界は光明そのものである。・・
・・この光明の世界、この相即相入の場面は、個物の世界である世間界との対照に於て、法界として知られている。・・・法界は真実の存在であって世間界から離れたものではないが、ただわれわれが菩薩の生きている霊的生活にまで至らないと法界と世間界とが全く同一だということにはならぬ。個の堅い外郭が溶け去り、有限性の感じがもうわれわれを悩ますことがなくなった時に始めて法界は実現する。この様な法界に入ることを説くものという意味で、「華厳経」はまた「入法界品」ともよばれるのである。』
大乗仏教の経典の中でも、華厳経は人間の思想を全く超えた不可思議な光景であると、大拙は記述していると同時に、これを極力理解するために、「法界」や「相即相入」という教義を詳細に記述しています。そして「相即相入の教義」の中で次のようにも記述しています。
『多くの人々にはそれらは余りにも空想的なものであるかの様に、また余りにも遠く常識の領域を越えているものであるかの様に見える。しかし、われわれが経に叙述せられた通りに菩薩の霊性的経験の中心事実を把握すれば、ここに画き出されるすべての光景が全く当然なものであるという考えがおこり、それらの中にもはや何の非合理性も見ないということになるであろう。』
この後の文章から「菩薩の霊性的経験の中心事実」というのは「相即相入」を直覚することなのですが、これを把握すれば、華厳の世界の光景は当然なものであると記述しています。これは私にとってきわめて重要なことで、次項で検討しますが、「華厳経の風景」に「お墨付」をいただいたようなものなのです。
さらにこの後の文章で、唐の則天武后が相即相入の意を把握するのに困難を感じた時に、華厳の碩学(せきがく、学問のひろく深い人の意)法蔵が、提示し説明した「燈火を鏡で囲った光の多重反射のたとえ」について記述しています。これはすでに「「重重無尽」が行き着く世界」で検討したので省略しますが、大拙のいう華厳経の舞台の光明の世界とは、この燈火を鏡で囲った光の多重反射の様相を意味しているのでしょう。
当時、鈴木大拙は「フラクタル」の概念など知る由しもないのですが、法蔵と同様、直覚で理解していたと考えられます。
なお以後の考察は「10.自己相似集合であることの証明」での考察と一部重複します。
外から見た大楼閣と内から見た大楼閣
いよいよクライマックスの第三篇に入ります。まず本論に入る前に今回の展示画像について少し考察します。ところで臨済宗妙心寺派の禅僧、仙崖義梵(せんがいぎぼん, 1750-1837)和尚が描いたという禅画「○△□」は、多くの方が見たことがあると思いますが、この究極の意味がおわかりでしょうか。
これについて、 私なりにイメージしたのが、今回の展示画像なのです。ただし円については、すでに「相即相入/事事無礙」や「9.自己相似集合の世界観」で展示していますので、ここでは省略します。その代わりに正三角形や正四角形のほか、さらに欲張って、正五角形と正六角形も描いてしまいました。このへんが私が凡人の域から抜け出られないところです。 さらに語呂がよいので、三角形は三つの三角形、四角形には四つ、五角形には五つ、六角形には六つのそれぞれの形を、互いに妨げあわないように「相即相入」を繰り返したものです。
電脳で描いていますので、相即相入を無限に繰り返すことができますが、内部が黒く塗りつぶされて、きたなくなりますので、 適当な反復回数でとどめています。これらの図形がどのように描かれるかを、 わかりやすく説明するために、 三角形と四角形について、反復回数一回の場合と二回の場合を下図に示します。
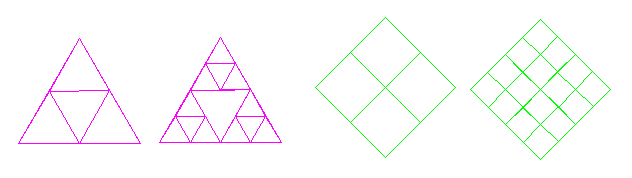
特に三角形の中に三つの三角形を繰り返し入れ込んだパターンは有名で、シェルピンスキー(ポーランドの数学者,1882-1969)のガスケット(ガスの漏れを防ぐパッキング)と呼ばれるもので、 自己相似集合の教材として、よく用いられる形です。
さて話を本論に戻しますが、「楼閣の描写」について、 鈴木大拙の記述を要約すると、楼閣は法界であること。 この法界の個多のものは完全な秩序が存すること。この秩序とは、『大楼閣の中には、また無量無数百千の楼閣がある。 その一々の楼閣がまた大楼閣そのものと同じ様にいみじく妙なる荘厳に飾られ、また空虚の如く広闊(こうかつ)である。しかしてまた、これらのすべての、その数、無量無数の楼閣は相互に障礙(しょうげ)するところさらになく、一々の楼閣はすべての諸処(しょしょ)の他の楼閣と完全に調和しつつしかもそれ自体の存在を保っている、一楼閣が他の楼閣と個々にまた全体的に融合することを妨げる何物もなく、そこには完全な相互交入があり、しかも完全な正整がある。若き求道者善財は自らを一々の楼閣の中に見ると共にまたすべての楼閣の中にも見るのである。すべては一々の中に含まれ、一々はすべてを含むからである。』
この鈴木大拙の記述と、展示画像のような自己相似集合との対応を考えるときに、もう一つの重要な概念を導入することが必要なのです。
それは西田幾多郎や鈴木大拙の思想の中心となる「真の自己とは何か」という概念です。 これも仏教思想に根ざしたものといわれていますが、自己と他者、およびその周囲環境(この場合は楼閣)が自己の内側に存在する世界、すなわちこれらが全て同一と直覚する境地を導入します。これで展示画像のような調和のとれた自己相似集合図形は、 まさに鈴木大拙の楼閣についての記述内容と完全に一致し、事事無礙法界と解釈できます。
以上自己相似集合は、 西田、鈴木の「自己究明」の概念を導入することで、 単なる幾何学図形から、 仏教思想の理想的な世界観を表現する図形へと生まれ変わるのです。そしてこれが善財童子が大楼閣の内部に入って(入法界)、直覚した大楼閣そのものであり、また「事事無礙法界」の構造であると考えられます。
そしてこの自己相似集合図形は、「相即相入」を反復・繰り返すことで作られるのでした。
この事事無礙法界の構造と考えられる自己相似集合は、「相即相入/ 事事無礙」ですでに考察をしていますが、 このような図形の原形は、 自己相似集合やフラクタルなどの概念が生まれるはるか以前、八世紀頃に、 金剛界曼茶羅として仏教界に存在していたことは、 みなさまには御存知のことと思います。
代表的な胎蔵・金剛界曼陀羅の図を見れば容易に理解できるように、大日如来を中心とした諸尊の集まりの場所であって、諸尊の大楼閣を象徴した図と考えるのが、もっとも素直で基本なのでしょう。この図に自己相似集合に近いものが存在することは、大楼閣の内部が自己相似集合であることを物語るものと考えられます。
また曼陀羅を構成する図形も、主に円や正方形で、これも楼閣やその城郭(じょうかく)を表しているのでしょう。また三角形も存在するといわれており、仙崖和尚の禅画「○△□」が頭をよぎり、これが楼閣を表している可能性もあります。
さて先に引用した鈴木大拙の記述、『法界(この場合は事事無礙法界と考えられます)は真実の存在であって世間界から離れたものではないが、ただわれわれが菩薩の生きている霊的生活にまで到らないと、法界と世間界とが全く同一だということにはならぬ。』とか『相即相入を直覚し、把握すれば華厳の世界の光景は当然なものである』という意味は、 相即相入から導かれる自己相似集合のような構造をいうのでしょう。さらにこのことに関して、 大変興味深い発見がありました。
大楼閣を内側から見た平面図は、 展示画像のような構造と考えられるのですが、ここで四角形の場合を注目しましょう。四角形に四つの四角形を相即相入した場合の配置図は、田の字構造なのです。
「不可思議神変事」といわれる大楼閣といえども、 我々凡人の住宅の室の配置の基本といえる田の字構造と何ら変わりがないのです。我々は各室を有効に利用するため、 室の空間を幾重にも細かく区切って、 そこに物を相即相入して、 収納庫として用いているのです。
田の字の個々の四角の中に、また田の字が入り、またその個々の四角に田の字が入るという繰り返しなのです。 これが大楼閣の内部の構造なのです。
最後に、 仙崖和尚が描いたという禅画「○△□」の究極の意味は、 外から見た大楼閣の平面図に他ならず、この外面的な○△□の図形の内側には 「相即相入」とか「重重無尽」や「事事無礙法界」などの華厳思想の核心が、 隠されていると直観したのですが、如何でしょう。